Introduction
Racing drones are becoming more and more popular, and it would not only be interesting to know, how fast they can really go, but also which parameters have a major impact on their maximum speed. When I searched in the net, I couldn’t find clear answers and had to work out something by myself; so here is my model. To be clear, my intention is not to get absolute precise numbers, but more to understand the physics behind, and to have a tool to get realistic estimates and comparisons of flight parameters for different quadcopter models. If you are not interested in the details, just scroll down to the end of the page, where I show the final formulas and some calculated examples.
Model
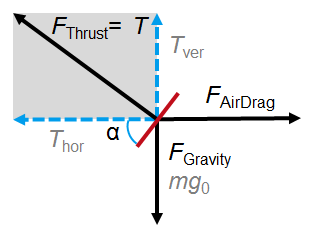
The model is based on classical mechanics, basically Newton’s second law of motion:
(1) ![]()
F are the forces for thrust, gravity and air drag,
m the mass (weight) of the quadcopter and
v the speed.
Thrust is defined as a force and measured in Newton. In datasheets motor thrust is usually shown as pull P in gram for selected propeller types, therefore it has to be multiplied by gravity: T = P * g0.
For the two special cases of a vertical climbing quadcopter, or – at a given altitude – forward flying quadcopter, based on (1) the following equations have to be solved:
(2a) Climbing ![]()
(2b) Forward flight ![]()
T is total motor thrust (N),
g0 gravity of earth (9.81 N),
ρ density of air (kg/m3),
cD drag coefficient and
Aeff effective area of the quadcopter (m2)
In both cases, due to the air drag, the quadcopter will reach a limit speed without further acceleration. We calculate this limit speed as maximum possible rate of climb (3a) or forward flight speed (3b):
(3a) ![]()
(3b) ![]()
The factor with the square root in (3b) reflects the fact that a certain fraction of the thrust is needed to keep the quadcopter at constant altitude. The vertical component of the motor thrust has to compensate the gravitational force mg0. The copter flies with a forward pitch angel α.
(4) Forward pitch angle ![]()
Maximum Rate of Climb
From (3a) we get the maximum rate of climb:
(5) 
A top area of the quadcopter (m2)
Introducing the thrust over weight ratio TR = T / (m·g0) we get the rate of climb as function of thrust ratio TR:
(5a) 
The thrust ratio has to be greater than 1. Beside the thrust ratio, the maximum climbing rate is a function of the weight (m) and the size (area A) of the quadcopter, as well as the aerodynamic drag coefficient cD.
Maximum forward flight speed
From (3b) we calculate the maximum forward flight speed as
(6)
Using the thrust ratio TR and substituting T = TR· m·g0 we get
(6a) 
The effective area Aeff is a function of the forward pitch angle α. To simplify the calculation we only take into account the vertical projection of the quadcopter top area
(7) ![]()
and as result we get
(8) 
(8a) 
For practical thrust ratios around 2 or higher the factor under the double square root is close to 1. As for the maximum rate of climb, the maximum forward flight speed depends on the weight, size and aerodynamic form of the quadcopter, but the main factor is the thrust over weight ratio. An increase will directly translate into an increase in forward speed.
Practical Examples
We now can use equations (5a) and (8a) for the estimation of the maximum rate of climb and the maximum forward speed of a quadcopter:


Air density is 1.2 kg/m3, g0 is 9.81 N, the drag coefficient is taken as 1.3; remaining input parameters are the thrust ratio TR, the weight m and top area A of the quadcopter. For the calculation of the thrust ratio we take 90% of the peak thrust, as there must be some reserve for the flight controller to level the quadcopter during flight. We approximate the top area A of the quadcopter based on the motor to motor distance MTM and the propeller size by
(9) ![]()
250 FPV Racing Quad
For a 250 racing quad (MTM = 0,255 m) of 560 g weight (455 g net + 105 g battery, m = 0.56 kg) with 2204-2300kv motor and 5 inch propeller (r = 0.0635 m), pull is specified as 310 g, resulting in a thrust ratio of TR = 2. We calculate a maximum flight speed of 18.5 m/s (67 km/h) and a maximum climbing rate of 10 m/s. Changing the propeller to 6 inch will increase pull to 440 g, resulting in a thrust ratio of 2.8. The speed will increase to 24.5 m/s (88 km/h).
180 FPV MiniQuad
I have built a mini quadcopter with 4 inch propeller and 180 mm MTM. Net weight is 245 g, total weight with 1.3 Ah battery is 365 g. The thrust ratio is 2.17 resulting in a maximum speed of 22 m/s (78 km/h). This mini quadcopter will be faster than the racing quad with 5 inch propellers.
DJI Phantom 2 Vision+
For the DJI Phantom 2 Vision+ MTM is 0.35 m, weight is 1.24 kg and propeller size 9 inch. With a thrust ratio of 1.9 we calculate a maximum flight speed of 17 m/s (61 km/h) and a maximum climbing rate of 9 m/s. The specification of the Phantom shows 15 m/s maximum speed and 6 m/s rate of climb. Practical tests show an actual climbing rate of 8 m/s.
Concluding Remarks
Though the model is rough with simplifications, it seems to give some realistic numbers. The result is not surprising: for a given model the major factors to increase speed are reducing weight (lighter battery), increasing thrust (change of propellers) or improving aerodynamics (reducing the drag coefficient).
The parameters with the highest uncertainty in the calculation are the actual effective area and the drag coefficient (Aeff cD). It would be interesting to get some actual measured values.
